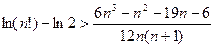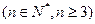已知函数
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设 的内角
的内角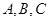 对边分别为
对边分别为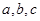 ,且
,且 ,
, ,
,
若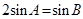 ,求
,求 的值.
的值.
(本小题满分14分)
已知数列 、
、 满足a1=1,a2=2,bn+1=3bn
满足a1=1,a2=2,bn+1=3bn ,bn=an+1-an.
,bn=an+1-an.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn.
(本小题满分14分)
已知函数 .
.
(1)若函数f(x)在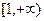 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(2)当a=1时,求f(x)在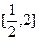 上的最大值和最小值;(注
上的最大值和最小值;(注 )
)
(3)当a=1时,求证:对大于1的任意正整数n,均有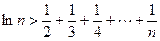 .
.
(本小题满分14分)
已知椭圆C的长轴长与短轴长之比为 ,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
(1)求椭圆C的标准方程;
(2)已知A(-3,0),B(3,0)P是椭圆C上异于A、B的任意一点,直线AP、BP分别交于y轴于M、N两点,求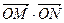 的值;
的值;
(3)在(2)的条件下,若G(s,o)、H(k,o)且 ,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
(本小题满分12分)
某辆载有4位乘客的公共汽车在到达终点前还有3个停靠点(包括终点站),若车上每位乘客在所剩的每一个停靠点下车的概率均为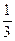 ,用
,用 表示这4位乘客在终点站下车的人数,求:
表示这4位乘客在终点站下车的人数,求:
(1)随机变量 的分布列;
的分布列;
(2)随机变量 的数学期望.
的数学期望.
函数

(1)求 的单调区间;
的单调区间;
(2)求使函数f(x)有零点的最小正整数a的值;
(3)证明: