(本小题满分14分)
已知数列 、
、 满足a1=1,a2=2,bn+1=3bn
满足a1=1,a2=2,bn+1=3bn ,bn=an+1-an.
,bn=an+1-an.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn.
已知半径为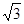 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
设椭圆 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率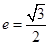 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且 .
.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线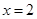 交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且 ,点C为圆O上一点,且
,点C为圆O上一点,且 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.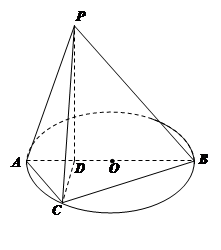
(1)求证: ;
;
(2)求二面角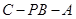 的余弦值.
的余弦值.
已知平行四边形的两条边所在直线的方程分别是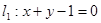 ,
, , 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
, 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.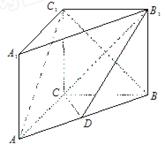
(1)求证: ∥平面
∥平面 ;
;
(2)求异面直线 与
与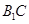 所成角的余弦值.
所成角的余弦值.