已知曲线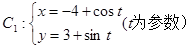
（t为参数），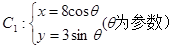
（1）化C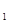
，C
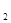的方程为普通方程，并说明它们分别表示什么曲线；
（2）若C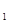上的点P对应的参数为
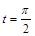，Q为C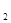上的动点，求
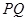中点
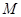到直线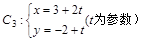
（t为参数）距离的最小值。
在极坐标中，已知圆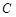
经过点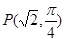
，圆心为直线
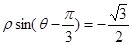与极轴的交点，求圆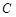的极坐标方程．
已知函数
的定义域为
，若
在
上为增函数，则称
为“一阶比增函数”.
(Ⅰ) 若
是“一阶比增函数”，求实数
的取值范围；
(Ⅱ) 若是“一阶比增函数”，求证：
，
；
（Ⅲ）若是“一阶比增函数”，且有零点，求证：
有解.
已知函数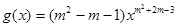
是幂函数且在
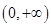上为减函数，函数
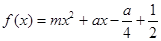在区间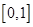
上的最大值为2，试求实数
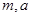的值。
设函数
.
（I）当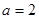
时，求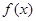
的单调区间；
（II）若
对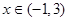
恒成立，求实数
的取值范围．
的周长为
，且
.
的长.
，①求
的正弦值. ②求
的值.