已知函数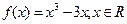
，又
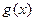由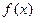
向右平移1个单位，向上平移2个单位得到.
（I）判断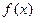的奇偶性，并求出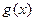的极大值与极小值之和.
（II）过点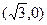
且方向向量为
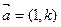的直线与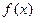的图像相切，求实数
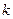的值.
|
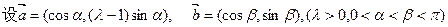是平面上的两个向量，且
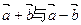互为垂直.
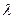的值；（2）若
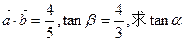的值.
已知函数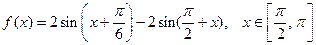
.
（1）若
，求函数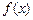
的值；（2）求函数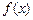的值域；
（3）求满足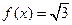
的自变量
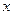的值.
设足球场宽65米，球门宽7米，当足球运动员沿边路带球突破，距底线多远处射门，对球门所张的角最大？（保留两位小数）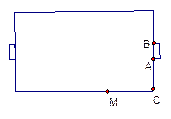
北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，在同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为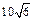
米（如图所示），旗杆底部与第一排在一个水平面上。若国歌长度约为50秒，问：升旗手应以多大的速度（米/秒）匀速升旗？
设计算法框图和程序，求1+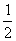
+
+
+
+
+…+
的值.