如图，四棱锥
中，
，
.
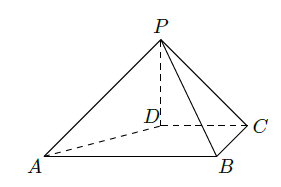
（1）求证：
（2）求点 到平面 的距离.
（本小题满分15分）
如图，已知椭圆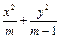
=1（2≤m≤5），过其左焦点且斜率为1的直线与椭圆及
直线
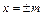的交点从左到右的顺序为A、B、C、D，设
．
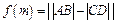（Ⅰ）求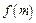
的解析式；
（Ⅱ）求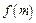的最值．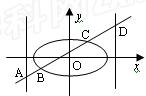
（本小题满分14分）
某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可以继续参加科目B的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目A成绩合格的概率均为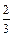
，每次考科目B成绩合格的概率均为
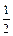。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试的次数为
．
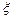（Ⅰ）求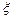的分布列和期望
；
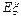（Ⅱ）求该同学在这项考试中获得合格证
书的概率．
如图，四棱锥P—ABCD的底面ABCD为一直角梯形，其中BA⊥AD，CD⊥AD，CD=AD=2AB，PA⊥底面ABCD，E是PC的中点．
（Ⅰ）求证：BE//平面PAD；
（Ⅱ）若BE⊥平面PCD。
（i）求异面直线PD与BC所成角的余弦值；
（ii）求二面角E—BD—C的余弦值．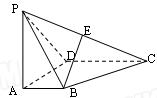
（本小题14分）
已知钝角△ABC中，角A、B、C的对边分别为a、b、c，且有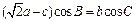
（Ⅰ）求角B的大小；
（Ⅱ）设向量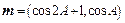
，
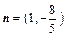，且m⊥n，求
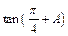的值．
（本小题满分16分）
设
、
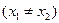是函数
的两个极值点．
（1）若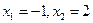
，求函数
的解析式；
（2）若
，求
的最大值；
（3）设函数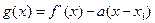
，
，当
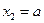时，
求证：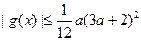
．