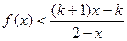设
使定义在区间
上的函数,其导函数为
.如果存在实数
和函数
,其中
对任意的
都有
,使得
,则称函数
具有性质
.
(1)设函数
,其中
为实数
①求证:函数
具有性质
;
②求函数
的单调区间
(2)已知函数
具有性质
,给定
,设
为实数.
,且
,若
,求
的取值范围
(本小题满分15分)已知
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)定义正数数列 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
|
(Ⅲ)令 成立的最小n值.
成立的最小n值.
已知函数 的一个极值点.
的一个极值点.
(Ⅰ)求 ;
;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若 的图象与x轴有且只有3个交点,求b的取值范围.
的图象与x轴有且只有3个交点,求b的取值范围.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.
(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)求证:平面PCE⊥平面PCD;
(Ⅲ)求三棱锥C-BEP的体积.
已知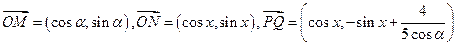
(1)当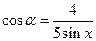 时,求函数
时,求函数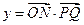 的最小正周期;
的最小正周期;
(2)当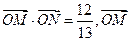 ∥
∥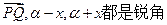 时,求
时,求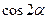 的值.
的值.
已知函数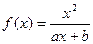 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;