(本小题满分13分)
专家通过研究学生的学习行为,发现学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设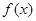 表示学生注意力随时间
表示学生注意力随时间 (分钟)的变化规律(
(分钟)的变化规律(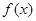 越大,表明学生注意力越大),经过试验分析得知:
越大,表明学生注意力越大),经过试验分析得知:
(Ⅰ)讲课开始后多少分钟,学生的注意力最集中?能坚持多少分钟?
(Ⅱ)讲课开始后5分钟时与讲课开始后25分钟时比较,何时学生的注意力更集中?
(Ⅲ)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲完这道题目?
在 中,
中, 、
、 、
、 所对的边分别是
所对的边分别是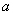 、
、 、
、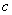 ,其中
,其中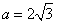 ,
,
 ,求角
,求角 的大小和三角形的面积
的大小和三角形的面积 .
.
(本小题满分14分)已知函数
(1)曲线 经过点P(1,2),且曲线C在点P处的切线平行于直线
经过点P(1,2),且曲线C在点P处的切线平行于直线 ,求a,b的值;
,求a,b的值;
(2)在(1)的条件下试求函数 的极小值;
的极小值;
(3)若 在区间(1,2)内存在两个极值点,求证:
在区间(1,2)内存在两个极值点,求证:
本小题满分14分)已知 中,点A、B的坐标分别为
中,点A、B的坐标分别为 ,点C在x轴上方。
,点C在x轴上方。
(1)若点C坐标为 ,求以A、B为焦点且经过点C的椭圆的方程;
,求以A、B为焦点且经过点C的椭圆的方程;
(2)过点P(m,0)作倾角为 的直线
的直线 交(1)中曲线于M、N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值。
交(1)中曲线于M、N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值。
(本小题满分13分)已知数列 中,
中, ,前n项和为
,前n项和为
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,求满足不等式
,求满足不等式 的n值。
的n值。
(本小题满分12分)某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系: ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)