(本小题满分13分)
已知函数 是定义在
是定义在 上的奇函数.
上的奇函数.
(Ⅰ)求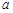 的值;
的值;
(Ⅱ)求函数 的值域;
的值域;
(Ⅲ)当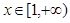 时,
时,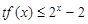 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题12分)设函数f(x)=a·b,其中a=(2cosx,1), b=(cosx, sin2x), x∈R.
sin2x), x∈R.
(1)若f(x)=1- ,且x∈[
,且x∈[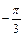 ,
,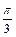 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(|m|<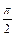 )平移后得到函数y= f(x)的图象,求实数m、n的值.
)平移后得到函数y= f(x)的图象,求实数m、n的值.
(本小题10分) 已知函数 在其一个周期内的图象上有一个最高点
在其一个周期内的图象上有一个最高点 和一个最低点
和一个最低点 。
。
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求 的单调增区间。
的单调增区间。
(本小题10分)已知 ,且
,且 .
.
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)求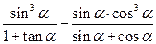 的值.
的值.
(本小题10分) 已知 ,
, ,当
,当 为何值时,
为何值时,
(Ⅰ)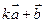 与
与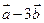 垂直?
垂直?
(Ⅱ) 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(本小题8分)每次抛掷一枚骰子(六个面上分别标以数字1,2,3,4,5,6)
(Ⅰ)连续抛掷2次,求向上的数不同的概率
(Ⅱ)连续抛掷2次,求向上的数之和为6的概率