如图,沿等腰直角三角形 的中位线
的中位线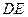 ,将平面
,将平面 折起,使得平面
折起,使得平面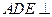 平面
平面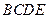 得到四棱锥
得到四棱锥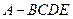 .
.
(1)求证:平面 平面
平面 ;
;
(2)过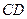 的中点
的中点 的平面
的平面 与平面
与平面 平行,试求平面
平行,试求平面 与四棱锥
与四棱锥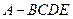 各个面的交线所围成多边形的面积与三角形
各个面的交线所围成多边形的面积与三角形 的面积之比。
的面积之比。
(3)求二面角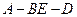 的余弦值。
的余弦值。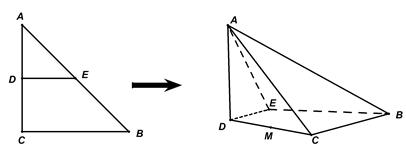
(1)学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;
(2)单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
| 损坏餐椅数 |
未损坏餐椅数 |
总 计 |
|
| 学习雷锋精神前 |
50 |
150 |
200 |
| 学习雷锋精神后 |
30 |
170 |
200 |
| 总计 |
80 |
320 |
400 |
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式: ,
,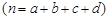
| P(K2≥k0) |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
复数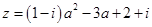 (
(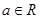 ),
),
(1)若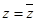 ,求
,求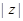 ;
;
(2)若在复平面内复数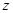 对应的点在第一象限,求
对应的点在第一象限,求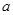 的范围.
的范围.
已知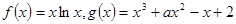
(Ⅰ)求函数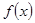 的单调区间;
的单调区间;
(Ⅱ)求函数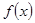 在
在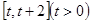 上的最小值;
上的最小值;
(Ⅲ)对一切的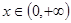 ,
,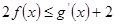 恒成立,求实数
恒成立,求实数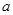 的取值范围.
的取值范围.
已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值还是极大值,并说明理由.
已知正数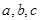 成等差数列,且公差
成等差数列,且公差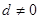 ,用反证法求证:
,用反证法求证: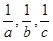 不可能是等差数列。
不可能是等差数列。