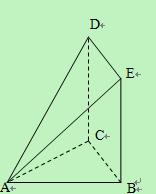
如图,已知四棱锥的底面为等腰梯形,,,垂足为,是四棱锥的高。

(Ⅰ)证明:平面平面;
(Ⅱ)若,60°,求四棱锥的体积。
已知数列 的前
的前 项和为
项和为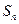 ,且
,且 (
( ).
).
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)若数列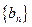 满足
满足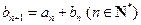 ,且
,且 ,求数列
,求数列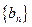 的通项公式.
的通项公式.
在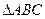 中,内角A,B,C的对边分别是
中,内角A,B,C的对边分别是
(I)求角C的大小;
(II)若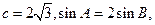 求a,b.
求a,b.
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵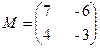 ,向量
,向量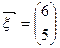 .
.
(I)求矩阵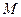 的特征值
的特征值 、
、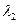 和特征向量
和特征向量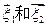 ;
;
(II)求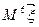 的值.
的值.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为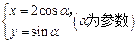 .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为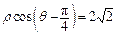 .
.
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
(3)(本小题满分7分)选修4-5:不等式选讲
(Ⅰ)已知:a、b、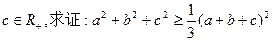 ;
;
(Ⅱ)某长方体从一个顶点出发的三条棱长之和等于3,求其对角线长的最小值.
(本小题满分13分)
已知数列 满足
满足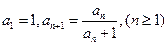 ,数列
,数列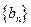 满足
满足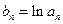 ,数列
,数列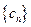
满足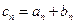 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ) ,
,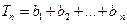 ,试比较
,试比较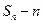 与
与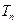 的大小,并证明;
的大小,并证明;
(Ⅲ)我们知道数列 如果是等差数列,则公差
如果是等差数列,则公差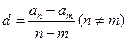 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列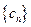 中,
中,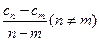 不是一个常数,但
不是一个常数,但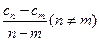 是否会小于等于一个常数
是否会小于等于一个常数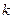 呢,若会,请求出
呢,若会,请求出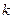 的范围,若不会,请说明理由.
的范围,若不会,请说明理由.
(本小题满分13分)
某设计部门承接一产品包装盒的设计(如图所示),客户除了要求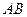 、
、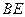 边的长分别为
边的长分别为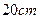 和
和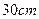 外,还特别要求包装盒必需满足:①平面
外,还特别要求包装盒必需满足:①平面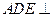 平面
平面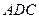 ;②平面
;②平面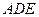 与平面
与平面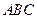 所成的二面角不小于
所成的二面角不小于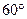 ;③包装盒的体积尽可能大。
;③包装盒的体积尽可能大。
若设计部门设计出的样品满足: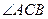 与
与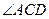 均为直角且
均为直角且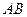 长
长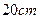 ,矩形
,矩形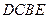 的一边长为
的一边长为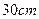 ,请你判断该包装盒的设计是否能符合客户的要求?说明理由.
,请你判断该包装盒的设计是否能符合客户的要求?说明理由.