在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.
(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
已知数列 的前
的前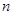 项和为
项和为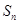 ,
,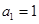 ,
, ,
,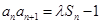 ,其中
,其中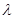 为常数.
为常数.
(1)证明: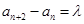 ;
;
(2)是否存在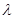 ,使得
,使得 为等差数列?并说明理由.
为等差数列?并说明理由.
如图,在△ABC中,∠ABC=90°,AB= ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
已知抛物线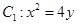 的焦点
的焦点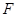 也是椭圆
也是椭圆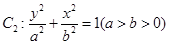 的一个焦点,
的一个焦点,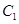 与
与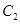 的公共弦的长为
的公共弦的长为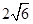 .
.
(1)求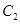 的方程;
的方程;
(2)过点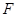 的直线
的直线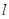 与
与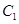 相交于
相交于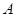 ,
,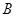 两点,与
两点,与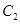 相交于
相交于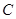 ,
,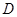 两点,且
两点,且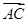 与
与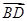 同向.
同向.
(ⅰ)若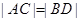 ,求直线
,求直线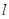 的斜率;
的斜率;
(ⅱ)设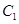 在点
在点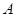 处的切线与
处的切线与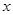 轴的交点为
轴的交点为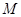 ,证明:直线
,证明:直线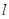 绕点
绕点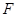 旋转时,
旋转时,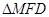 总是钝角三角形.
总是钝角三角形.
已知数列 满足
满足 ,
, .
.
(1)若 为递增数列,且
为递增数列,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)若 ,且
,且 是递增数列,
是递增数列, 是递减数列,求数列
是递减数列,求数列 的通项公式.
的通项公式.
如图,在四棱锥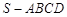 中,底面
中,底面 是正方形,
是正方形,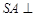 底面
底面 ,
,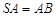 , 点
, 点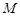 是
是 的中点,
的中点, ,且交
,且交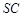 于点
于点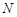 .
.
(Ⅰ)求证: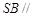 平面
平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅲ)求二面角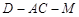 的余弦值.
的余弦值.