一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分ξ的数学期望Eξ.
已知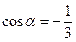 ,
,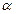 为第二象限角,求
为第二象限角,求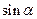 和
和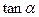 及
及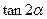 的值.
的值.
.(本小题满分15分)
已知函数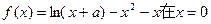 处取得极值。
处取得极值。
(1)求实数a的值;
(2)求函数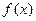 的单调区间;
的单调区间;
(3)若关于x的方程
 在区间(0,2)有两个不等实根,求实数b的取值范围。
在区间(0,2)有两个不等实根,求实数b的取值范围。
(本小题满分15分)已知点P(4,4),圆C: 与椭圆E:
与椭圆E: 有一个公共点A(3,1),F1.F2分别
有一个公共点A(3,1),F1.F2分别 是椭圆的左.右焦点,直线PF1与圆C相切.
是椭圆的左.右焦点,直线PF1与圆C相切.
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求 的范围.
的范围.
本小题满分14分)如图,四棱锥E—ABCD中,ABCD是矩形,平面EAB 平面ABCD,AE=EB=BC=2,F为CE上的点,
平面ABCD,AE=EB=BC=2,F为CE上的点,
且BF 平面ACE.
平面ACE.
(1)求证:AE BE;
BE;
(2)求三棱锥D—AEC的体积;
(3)求二面角A—CD—E的余弦值.
(本小题满分14分)
已知数列 中,
中, ,
, ,其前
,其前 项和
项和 满足
满足 ,令
,令 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求证:
,求证: (
( ).
).