.(本小题满分15分)
已知函数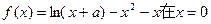 处取得极值。
处取得极值。
(1)求实数a的值;
(2)求函数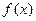 的单调区间;
的单调区间;
(3)若关于x的方程
 在区间(0,2)有两个不等实根,求实数b的取值范围。
在区间(0,2)有两个不等实根,求实数b的取值范围。
已知函数f(x)=  +2sin2x
+2sin2x
(1)求函数f(x)的最大值及此时x的值;
(2)求函数f(x)的单调递减区间。
若不等式1-loga <0有解,则实数a的范围是 .
<0有解,则实数a的范围是 .
已知函数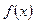 与函数
与函数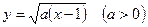 的图像关于直线
的图像关于直线 对称.
对称.
(1)试用含 的代数式表示函数
的代数式表示函数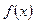 的解析式,并指出它的定义域;
的解析式,并指出它的定义域;
(2)数列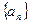 中,
中,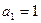 ,当
,当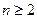 时,
时, .数列
.数列 中,
中,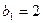 ,
,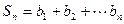 .点
.点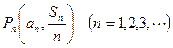 在函数
在函数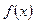 的图像上,求
的图像上,求 的值;
的值;
(3)在(2)的条件下,过点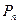 作倾斜角为
作倾斜角为 的直线
的直线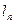 ,则
,则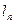 在y轴上的截距为
在y轴上的截距为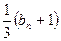
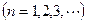 ,求数列
,求数列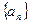 的通项公式.
的通项公式.
在平面直角坐标系中,已知A1(-3,0),A2(3,0),P(x,y),M( ,0),若实数λ使向量
,0),若实数λ使向量 ,λ
,λ ,
,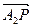 满足λ2·(
满足λ2·( )2=
)2= ·
·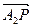 。
。
(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当λ=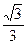 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
已知:以点C (t, )(t∈R , t≠ 0)为圆心的圆与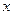 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.