无锡学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设ξ为选出的人中既会唱歌又会跳舞的人数,且P(ξ>0)=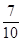
(1)求文娱队的队员人数;
(2)写出ξ的概率分布列并计算E(ξ).
(本小题满分10分)
选修4-1:几何证明选讲
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,
求证:BE•BF=BC•BD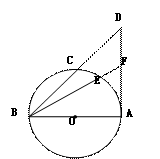
(本小题满分10分)
如图所示,四边形ABCD是矩形,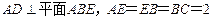 ,F为CE上的点,且BF
,F为CE上的点,且BF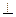 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G
求证:AE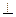 平面BCE
平面BCE
求证:AE//平面BFD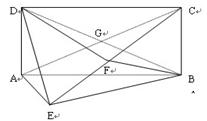
(本小题满分10分)
椭圆C: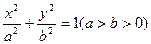 的两个焦点为
的两个焦点为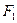 、
、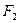 ,点
,点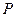 在椭圆C上,且
在椭圆C上,且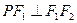 ,
,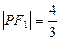 ,
,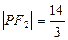 .
.
(1) 求椭圆C的方程;
(2) 若直线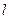 过圆
过圆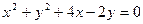 的圆心
的圆心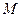 ,交椭圆C于
,交椭圆C于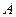 、
、 两点,且
两点,且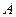 、
、 关于点
关于点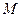 对称,求直线
对称,求直线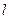 的方程.
的方程.
(本小题满分12分)
已知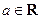 ,函数
,函数 .
.
(1)若函数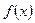 在区间
在区间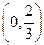 内是减函数,求实数
内是减函数,求实数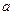 的取值范围;
的取值范围;
(2)求函数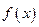 在区间
在区间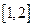 上的最小值
上的最小值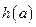 ;
;
(3)对(2)中的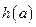 ,若关于
,若关于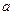 的方程
的方程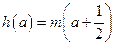 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数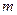 的取值范围.
的取值范围.
(本小题满分12分)
已知函数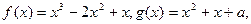 若函数
若函数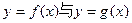 的图像有三个不同的交点,求实数a的取值范围。
的图像有三个不同的交点,求实数a的取值范围。