设函数
.
(Ⅰ)证明:当
时,
;
(Ⅱ)设当
时,
,求
的取值范围.
同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为 .
.
(1)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
(2)求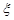 的数学期望和方差.
的数学期望和方差.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间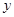 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出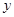 关于
关于 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工 个零件需要多少时间?
个零件需要多少时间?
参考公式:回归直线 ,其中
,其中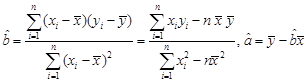 .
.
一个布袋里有3个红球,2个白球共5个球. 现抽取3次,每次任意抽取2个,并待放回后再抽下一次.求:
(1)3次抽取中,每次取出的2个球都是1个白球和1个红球的概率;
(2)3次抽取中,有2次取出的2个球是1个白球和1个红球,还有1次取出的2个球同色的概率.
其中第(1)(2)问文理科学生都要做,第(3)问按题目要求分文理来做。
已知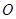 为坐标原点,向量
为坐标原点,向量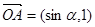 ,
,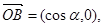
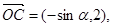 点
点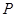 是直线
是直线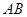 上的一点,且
上的一点,且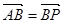 .
.
求点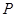 的坐标(用
的坐标(用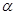 表示);
表示);
若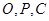 三点共线,求以线段
三点共线,求以线段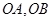 为邻边的平行四边形的对角线长;
为邻边的平行四边形的对角线长;
(3)(文科生做)记函数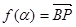 •
•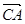 ,且
,且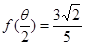 ,求
,求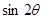 的值.
的值.
(3)(理科生做)记函数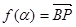 •
•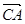 ,
,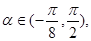 讨论函数
讨论函数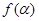 的单调性,并求其值域.
的单调性,并求其值域.
在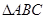 中,角
中,角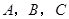 所对的边分别为
所对的边分别为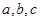 ,且
,且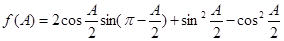
(1)求函数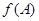 的最大值;
的最大值;
(2)若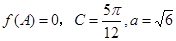 ,求
,求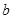 的值.
的值.