给出下面的数表序列,其中表
有
行,第1行的
个数是1,3,5,…,2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。

(1)写出表4,验证表4各行中的数的平均数按从上到下的顺序构成等比数列,并将结论推广到表 (不要求证明);
(2)每个数表中最后一行都只有一个数,它们构成数列1,4,12,…,记此数列为 ,求和: .
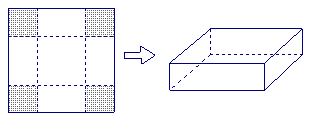
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
 |
设工厂到铁路线的垂直距离为20km,垂足为B.铁路线上距离B为100km处有一原料供应站C,现要在铁路BC之间某处D修建一个原料中转车站,再由车站D向工厂修一条公路.如果已知每千米的铁路运费与公路运费之比为3:5,那么,D应选在何处,才能使原料供应站C运货到工厂A所需运费最省?
若电灯B可在桌面上一点O的垂线上移动,桌面上有与点O距离为 的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(
的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?( 照度与
照度与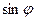 成正比,与
成正比,与 成反比)
成反比)
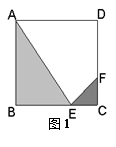
某人定制了一批地砖. 每块地砖 (如图1所示)是边长为 米的正方形
米的正方形 ,点E、F分别在边BC和CD上, △
,点E、F分别在边BC和CD上, △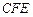 、△
、△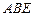 和四边形
和四边形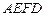 均由单一材料制成,制成△
均由单一材料制成,制成△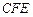 、△
、△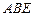 和四边形
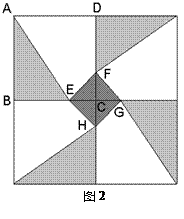
和四边形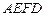 的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形
的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形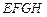 .
.
(1) 求证:四边形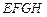 是正方形;
是正方形;
(2)  在什么位置时,定制这批地砖所需的材料费用最省?
在什么位置时,定制这批地砖所需的材料费用最省?
某产品按质量分为10个档次,生产第一档(即最低档次)的利润是每件8元,每提高一个档次,利润每件增加2元,但在相同的时间内产量减少3件.在相同的时间内,最低档的产品可生产60件.问在相同的时间内,生产第几档次的产品的总利润最大?有多少元?