某射手每次射击击中目标的概率是 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求 的分布列。
的分布列。
某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m﹣n|>10”概率.
已知函数 (其中
(其中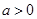 且
且 ),
), 是
是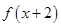 的反函数.
的反函数.
(1)已知关于 的方程
的方程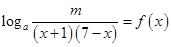 在
在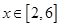 上有实数解,求实数
上有实数解,求实数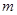 的取值范围;
的取值范围;
(2)当 时,讨论函数
时,讨论函数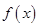 的奇偶性和单调性;
的奇偶性和单调性;
(3)当 ,
,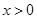 时,关于
时,关于 的方程
的方程 有三个不同的实数解,求
有三个不同的实数解,求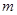 的取值范围.
的取值范围.
设幂函数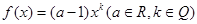 的图像过点
的图像过点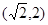 .
.
(1)求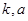 的值;
的值;
(2)若函数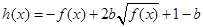 在
在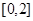 上的最大值为
上的最大值为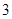 ,求实数
,求实数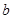 的值.
的值.
某工厂某种航空产品的年固定成本为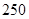 万元,每生产
万元,每生产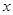 件,需另投入成本为
件,需另投入成本为 ,当年产量不足
,当年产量不足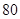 件时,
件时,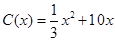 (万元).当年产量不小于
(万元).当年产量不小于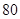 件时,
件时,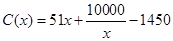 (万元).每件商品售价为
(万元).每件商品售价为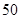 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量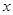 (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
已知不等式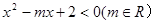 的解集为
的解集为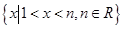 ,函数
,函数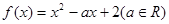 .
.
(1)求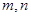 的值;
的值;
(2)若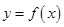 在
在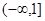 上单调递减,解关于
上单调递减,解关于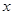 的不等式
的不等式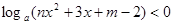 .
.