已知以原点
为中心,
为右焦点的双曲线
的离心率
.
(I)求双曲线
的标准方程及其渐近线方程;
(II)如题图,已知过点
的直线
与过点
(其中
)的直线
的交点
在双曲线
上,直线
与两条渐近线分别交与
两点,求
的面积.

(满分14分)
对于在区间A上有意义的两个函数 ,如果对任意的
,如果对任意的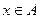 ,恒有
,恒有 在A上是接近的,否则称
在A上是接近的,否则称 在A上是非接近的。
在A上是非接近的。
(1)证明:函数 上是接近的;
上是接近的;
(2)若函数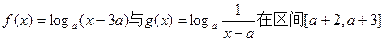 上是接近的,求实数a的取值范围。
上是接近的,求实数a的取值范围。
(满分12分)
已知数列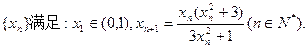
(1)证明:对任意的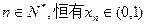 ;
;
(2)对于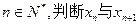 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。
(满分12分)
设
(1)若 的取值范围;
的取值范围;
(2)若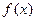 在区间[0,1]上的最小值为
在区间[0,1]上的最小值为 的值。
的值。
(满分12分)
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价P与上市时间t满足关系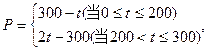 西红柿的种植成本Q与上市时间t满足关系
西红柿的种植成本Q与上市时间t满足关系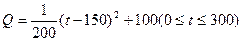 (市场售价与种植成本的单位是:元/100kg,时间单位是:天)。若认定市场售价减去种植成本为纯收益,问:何时上市的西红柿纯收益最大?
(市场售价与种植成本的单位是:元/100kg,时间单位是:天)。若认定市场售价减去种植成本为纯收益,问:何时上市的西红柿纯收益最大?
(满分12分)
设全集是实数集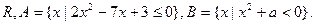
(1)当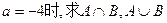 ;
;
(2)若 的取值范围。
的取值范围。