为了了解一个小水库中养殖的鱼有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：千克），并将所得数据分组，画出频率分布直方图（如图所示）
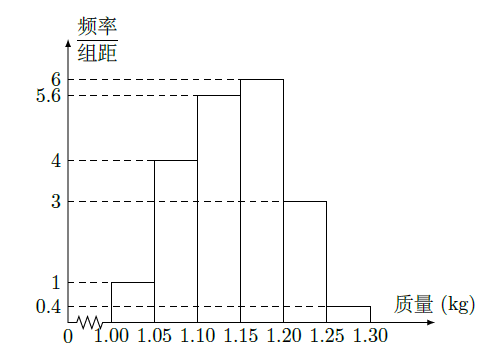
（Ⅰ）在答题卡上的表格中填写相应的频率；
（Ⅱ）估计数据落在（1.15,1.30）中的概率为多少；
（Ⅲ）将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数。
(本小题满分12分)
在△ABC中，内角A、B、C所对边的长分别为a、b、c，已知向量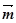
="(1,cosA" -1)，
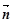=(cosA,1)且满足⊥.
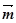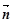（Ⅰ）求A的大小；
（Ⅱ）若a=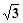
，b+c=3 求b、c的值.
本小题满分10分）设函数
，
（Ⅰ）求函数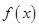
的最大值和最小正周期.，
（Ⅱ）设A,B,C为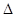
ABC的三个内角，若
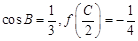，且C为锐角，求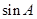
已知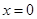
是函数
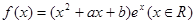的一个极值点，且函数
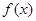的图象在
处的切线的斜率为2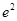
.
（Ⅰ）求函数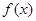的解析式并求单调区间.
（Ⅱ）设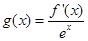
，其中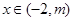
，问：对于任意的
,方程
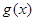
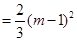在区间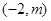
上是否存在实数根？若存在，请确定实数根的个数.若不存在，请说明理由.
（本小题满分14分）
如图，四棱锥P—ABCD中，PB⊥底面ABCD，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA。
（1）求直线PC与平面PAD所成角的余弦值；
（2）求证：PC//平面EBD；
（3）求二面角A—BE—D的余弦值.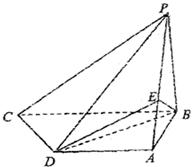
（本小题满分14分）
如图，A，B是海面上位于东西方向相距
海里的两个观测点，现位于A点北偏东
45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距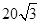
海里的C点的救援船立即即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？