．．已知动圆P过点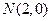
并且与圆
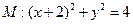相外切，动圆圆心P的轨迹为W，过点N的直线
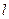与轨迹W交于A、B两点。
（1）求轨迹W的方程；
（2）若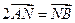
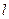，求直线的方程；
（3）对于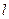的任意一确定的位置，在直线
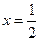上是否存在一点Q，使得
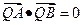，并说明理由。
在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：
摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱。
（1）摸出的3个球为白球的概率是多少？
（2）摸出的3个球为2个黄球1个白球的概率是多少？
（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？
已知函数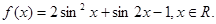
（1）求
的最小正周期及取得最大值时x的集合；
（2）在平面直角坐标系中画出函数在
上的图象.
已知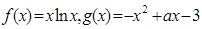
（1）求函数
在
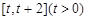上的最小值
（2）对一切的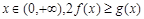
恒成立，求实数a的取值范围
（3）证明对一切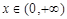
，都有
成立
已知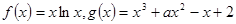
(Ⅰ)如果函数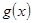
的单调递减区间为
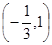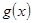,求函数的解析式;
(Ⅱ)对一切的
,
恒成立,求实数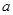
的取值范围
为了在夏季降温和冬季供暖时减少能源损耗，房屋的房顶和外墙需要建造隔热层，某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元，该建筑物每年的能源消耗费用为C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=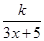
（0
x10），若不建隔热层，每年能源消耗费用为8万元。设f（x）为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式；
(2)隔热层修建多厚时，总费用f（x）达到最小，并求最小值。