在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪一组获奖率较高?
淘宝卖家在某商品的所有买家中,随机选择男女买家各50名进行调查,他们的评分等级如下表:
(1)从评分等级为(4,5]的人中随机选取两人,求恰有一人是男性的概率;
(2)规定:评分等级在[0,3]内为不满意该商品,在(3,5]内为满意该商品.完成下列2×2列联表并帮助卖家判断:能否在犯错误的概率不超过0.05的前提下认为满意该商品与性别有关系?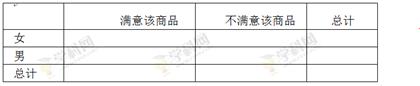
参考数据:
(参考公式: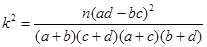 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
已知函数 ,
,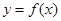 在
在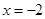 时有极值,在
时有极值,在 处的切线方程为
处的切线方程为 .
.
(1)求a,b,c
(2)求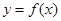 在
在 上的最大值.
上的最大值.
通过市场调查,得到某种产品的资金投入x万元与获得的利润y万元的数据,如表所示:
(1)根据上表提供的数据,用最小二乘法求线性回归方程;
(2)现投入资金10万元,求获得利润的估计值为多少万元?
(参考公式: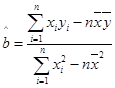 ,
,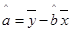 )
)
设函数

(1)证明: ;
;
(2)若 ,求m的取值范围.
,求m的取值范围.
在直角坐标系xOy中,以原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ(sinθ+cosθ)=1,曲线C2的参数方程为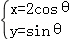 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1的直角坐标方程与曲线C2的普通方程;
(Ⅱ)试判断曲线C1与C2是否存在两个交点?若存在,求出两交点间的距离;若不存在,说明理由.