已知数列
中,
.
(Ⅰ)设
,求数列
的通项公式;
(Ⅱ)求使不等式
成立的
的取值范围.
如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(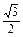 ,
, ,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
(1)求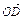 的坐标;
的坐标;
(2)设 和
和 的夹角为
的夹角为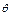 ,求cos
,求cos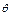 的值.
的值.
已知六面体ABCD—A′B′C′D′是平行六面体.
(1)化简
 +
+ +
+
 ,并在图上标出其结果;
,并在图上标出其结果;
(2)设M是底面ABCD的中心,N是侧面BCC′B′对角线BC′上的 分点,设
分点,设 =
=
 +
+
 +
+
 ,试求
,试求 ,
, ,
, 的值.
的值.
(1)求与向量a=(2,-1,2)共线且满足方程a·x=-18的向量x的坐标;
(2)已知A、B、C三点坐标分别为(2,-1,2),(4,5,-1),(-2,2,3),求点P的坐标使得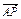 =
=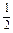 (
(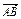 -
- );
);
(3)已知a=(3,5,-4),b=(2,1,8),求:①a·b;②a与b夹角的余弦值;
③确定 ,
, 的值使得
的值使得 a+
a+ b与z轴垂直,且(
b与z轴垂直,且( a+
a+ b)·(a+b)=53.
b)·(a+b)=53.
如图所示,已知空间四边形ABCD的各边和对角线的长都等于a,点M、N分别是AB、CD的中点.
(1)求证:MN⊥AB,MN⊥CD;
(2)求MN的长;
(3)求异面直线AN与CM所成角的余弦值.
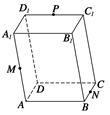
如图所示,在平行六面体ABCD-A1B1C1D1中,设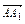 =a,
=a,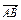 =b,
=b,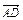 =c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
(1)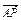 ;(2)
;(2)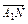 ;(3)
;(3)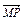 +
+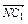 .
.