在边长为
的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥．
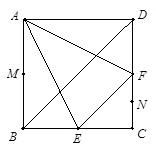
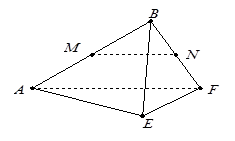
（1）判别MN与平面AEF的位置关系，并给出证明；
（2）证明AB⊥平面BEF；
（3）求多面体E-AFNM的体积．
（本小题满分10分）选修4-1：几何证明选讲
如图，四边形ABDC内接于圆，
，过C点的圆的切线与AB的延长线交于E点.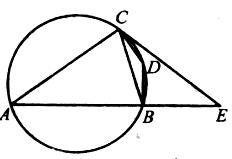
（1）求证：
；
（2）若
，
，
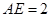，求AB的长.
（本小题满分12分）已知函数
，
，直线
与曲线
切于点
且与曲线
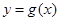切于点
.
（1）求a，b的值和直线的方程；
（2）证明：除切点外，曲线
、
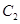位于直线的两侧.
（本小题满分12分）已知抛物线
，过点
的直线
交抛物线于A，B两点，坐标原点为O，
.
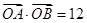（1）求抛物线的方程；
（2）当以AB为直径的圆与y轴相切时，求直线的方程.
为了调查某校学生体质健康达标情况，现采用随机抽样的方法从该校抽取了m名学生进行体育测试. 根据体育测试得到了这m名学生各项平均成绩（满分100分），按照以下区间分为七组：
，
，并得到频率分布直方图（如图），已知测试平均成绩在区间
有20人.
（1）求m的值及中位数n；
（2）若该校学生测试平均成绩小于n，则学校应适当增加体育活动时间，根据以上抽样调查数据，该校是否需要增加体育活动时间？
（本小题满分12分）如图，四棱锥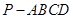
的底面ABCD是平行四边形，
底面ABCD，
，
.
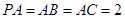（1）求证：
；
（2）点E是棱PC的中点，求点B到平面EAD的距离.