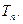(本小题共12分)如图,一张平行四边形的硬纸片 中,
中, ,
,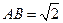 。沿它的对角线
。沿它的对角线 把△
把△ 折起,使点
折起,使点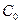 到达平面
到达平面 外点
外点 的位置。
的位置。
(Ⅰ)证明:平面 平面
平面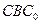 ;
;
(Ⅱ)如果△ 为等腰三角形,求二面角
为等腰三角形,求二面角 的大小。
的大小。
椭圆的中心在原点,焦点在x轴上,焦距为2,且经过点A 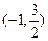 ;
;
(1)求满足条件的椭圆方程;
(2)求该椭圆的顶点坐标,长轴长,短轴长,离心率.
(本小题满分12分) 的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知
的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知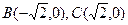 ,内切圆圆心
,内切圆圆心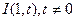 ,设点A的轨迹为L。(1)求L的方程;
,设点A的轨迹为L。(1)求L的方程; (2)过点C的动直线
(2)过点C的动直线 交曲线L于不同的两点M、N,问在
交曲线L于不同的两点M、N,问在 轴上是否存在一定点Q(Q不与C重合),使
轴上是否存在一定点Q(Q不与C重合),使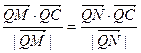 恒成立,若存在,试求出Q点的坐标,若不存在,说明理由。
恒成立,若存在,试求出Q点的坐标,若不存在,说明理由。
(本小题满分12分)袋中有分别写着“团团”和“圆圆”的两种玩具共7个,且形状完全相同,从中任取2个玩具都是“圆圆”的概率为 ,A、B两人不放回从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,……直到两人中有一人取到“圆圆”时即停止游戏,每个玩具在每一次被取出的机会是均等的,用
,A、B两人不放回从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,……直到两人中有一人取到“圆圆”时即停止游戏,每个玩具在每一次被取出的机会是均等的,用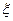 表示游戏终止时取玩具的次数。(1)求袋中“圆圆
表示游戏终止时取玩具的次数。(1)求袋中“圆圆 ”的个数;(2)求
”的个数;(2)求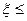 3的概率。
3的概率。
(本小题满分12分)
设函数
(1)若函数 在
在 内没有极值点,求
内没有极值点,求 的取值范围。
的取值范围。
(2)若对任意的 ,不等式
,不等式 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。
(本小题满分12分)数列 中,
中,
(1)求 的通项公式;(2)设
的通项公式;(2)设 ,求
,求