(本小题满分12分)袋中有分别写着“团团”和“圆圆”的两种玩具共7个,且形状完全相同,从中任取2个玩具都是“圆圆”的概率为 ,A、B两人不放回从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,……直到两人中有一人取到“圆圆”时即停止游戏,每个玩具在每一次被取出的机会是均等的,用
,A、B两人不放回从袋中轮流摸取一个玩具,A先取,B后取,然后A再取,……直到两人中有一人取到“圆圆”时即停止游戏,每个玩具在每一次被取出的机会是均等的,用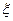 表示游戏终止时取玩具的次数。(1)求袋中“圆圆
表示游戏终止时取玩具的次数。(1)求袋中“圆圆 ”的个数; (2)求
”的个数; (2)求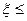 3的概率。
3的概率。
(本小题满分14分)
已知函数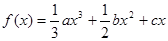
(Ⅰ)若函数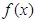 有三个零点
有三个零点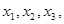 且
且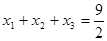 ,
,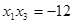 ,且
,且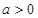 ,求函数
,求函数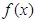 的单调区间;
的单调区间;
(Ⅱ)若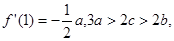 试问:导函数
试问:导函数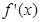
 在区间
在区间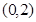 内是否有零点,并说明理由;
内是否有零点,并说明理由;
(Ⅲ)在(Ⅱ)的条件下,若导数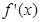 的两个零点之间的距离不小于
的两个零点之间的距离不小于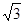 ,求
,求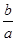 的取值范围。
的取值范围。
(本小题满分14分)
已知等差数列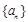 的公差
的公差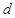 大于
大于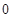 ,且
,且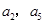 是方程
是方程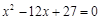 的两
的两 根,数列
根,数列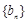 的前n项和为
的前n项和为 .
.
(Ⅰ) 求数列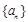 、
、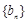 的通项公式;
的通项公式;
(Ⅱ)记 的前n项和
的前n项和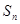 。
。
(本小题满分13分)
已知在函数 的图像上以
的图像上以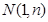 为切点的切线的倾斜角为
为切点的切线的倾斜角为
(Ⅰ)求 的值;
的值;
(Ⅱ)若方程 有三个不同实根,求
有三个不同实根,求 的取值范围;
的取值范围;
(Ⅲ)是否存在最小的正整数 ,使得不等式
,使得不等式 ,对
,对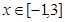 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数
 ;如果不存在,请说明理由。
;如果不存在,请说明理由。
.(本小题满分13分)
在 中,角
中,角 所对的边分别为
所对的边分别为 。已知
。已知
(Ⅰ)求 的值;
的值;
(Ⅱ)当 时,求
时,求 的长以及
的长以及 的面积
的面积 的值。
的值。
(本小题满分13分)
已知数列 是等比数列
是等比数列 数列
数列 是等差数列,
是等差数列,

(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 ;
;
(Ⅲ)设 ,
,
 比较
比较 与
与 大小,并证明你的结论。
大小,并证明你的结论。