某厂工人在2006年里有1个季度完成生产任务,则得奖金300元;如果有2个季度完成生产任务,则可得奖金750元;如果有3个季度完成生产任务,则可得奖金1260元;如果有4个季度完成生产任务,可得奖金1800元;如果工人四个季度都未完成任务,则没有奖金,假设某工人每季度完成任务与否是等可能的,求他在2006年一年里所得奖金的分布列.
对于函数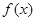 ,若在定义域内存在实数
,若在定义域内存在实数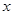 ,满足
,满足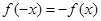 ,则称
,则称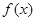 为“局部奇函数”.
为“局部奇函数”.
(Ⅰ)已知二次函数 ,试判断
,试判断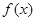 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(Ⅱ)若 是定义在区间
是定义在区间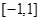 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(Ⅲ)若 为定义域
为定义域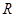 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
已知椭圆 的长轴两端点分别为
的长轴两端点分别为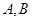 ,
, 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在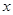 轴下方作矩形
轴下方作矩形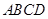 ,使
,使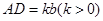 ,
,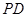 交
交 于点
于点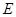 ,
,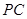 交
交 于点
于点 .
.
(Ⅰ)如图(1),若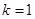 ,且
,且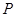 为椭圆上顶点时,
为椭圆上顶点时, 的面积为12,点
的面积为12,点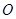 到直线
到直线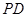 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)如图(2),若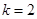 ,试证明:
,试证明: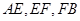 成等比数列.
成等比数列.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线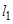 排,在路南侧沿直线
排,在路南侧沿直线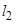 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将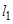 与
与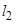 接通.已知
接通.已知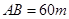 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的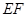 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设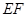 与
与 所成的小于
所成的小于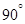 的角为
的角为 .
.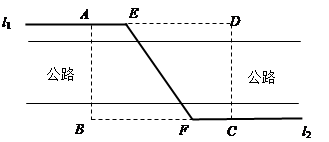
(Ⅰ)求矩形区域 内的排管费用
内的排管费用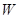 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)求排管的最小费用及相应的角 .
.
设数列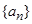 的前
的前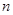 项和为
项和为 ,对任意
,对任意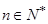 满足
满足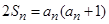 ,且
,且 .
.
(Ⅰ)求数列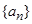 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列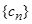 的前
的前 项和
项和 .
.
如图,四棱锥 的底面为矩形,
的底面为矩形, ,
, ,
, 分别是
分别是 的中点,
的中点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 .
.