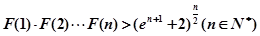在椭圆 上找一点,使这一点到直线
上找一点,使这一点到直线 的距离的最小值。
的距离的最小值。
在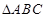 中,
中, 分别为角
分别为角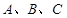 的对边,△ABC的面积S满足
的对边,△ABC的面积S满足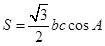 .
.
(1)求角 的值;
的值;
(2)若 ,设角
,设角 的大小为
的大小为 用
用 表示
表示 ,并求
,并求 的取值范围.
的取值范围.
已知 (a是常数,a∈R)
(a是常数,a∈R)
(Ⅰ)当a=1时求不等式 的解集;
的解集;
(Ⅱ)如果函数 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.
已知直线是过点 ,方向向量为
,方向向量为 的直线,圆方程
的直线,圆方程
(1)求直线的参数方程
(2)设直线与圆相交于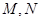 两点,求
两点,求 的值
的值
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD.
(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED= ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
已知函数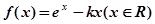
(1)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(2)若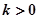 且对任意
且对任意 ,
, 恒成立,试确定实数
恒成立,试确定实数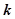 的取值范围;
的取值范围;
(3)设函数 ,求证:
,求证: