设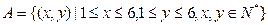
(1)求从A中任取一个元素是(1,2)的概率;
(2)从A中任取一个元素,求 的概率
的概率
(理)(3)设 为随机变量,
为随机变量,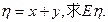
(2)设从A中任取一个元素, 的事件为C,有
的事件为C,有
(4,6)(6,4)(5,5)(5,6)(6,5)(6,6)
( 13分)已知函数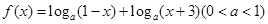
(1)求函数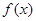 的定义域;
的定义域;
(2)求函数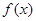 的零点;
的零点;
(3)若函数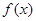 的最小值为-4,求a的值.
的最小值为-4,求a的值.
( 13分)已知
(1)求函数 的解析式
的解析式
(2)判断函数 的奇偶性
的奇偶性
(3)解不等式
( 13分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
(12分)已知函数 ,
,
(1)判断函数 的单调性,并利用单调性定义证明;
的单调性,并利用单调性定义证明;
(2)求函数 的最大值和最小值.
的最大值和最小值.
求 值:
(1) (2)
(2)