已知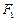 ,
,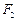 分别是双曲线
分别是双曲线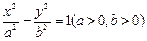 的左右焦点,以坐标原点
的左右焦点,以坐标原点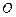 为圆心,以双曲线的半焦距
为圆心,以双曲线的半焦距 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为 ,与
,与 轴正半轴的交点为
轴正半轴的交点为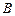 ,点
,点 在
在 轴上的射影为
轴上的射影为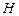 ,且
,且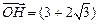
 .
.
⑴求双曲线的离心率;
⑵若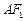 交双曲线于点
交双曲线于点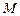 ,且
,且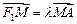 ,求
,求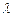 .
.
(本小题满分12分)已知定义在实数集 上的奇函数
上的奇函数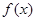 有最小正周期2,且当
有最小正周期2,且当 时,
时,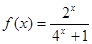
(Ⅰ)求函数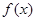 在
在 上的解析式;(Ⅱ)判断
上的解析式;(Ⅱ)判断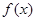 在
在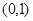 上的单调性;
上的单调性;
(Ⅲ)当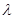 取何值时,方程
取何值时,方程 在
在 上有实数解?
上有实数解?
(本小题满分8分)已知平面向量a ,b
,b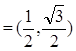
(Ⅰ)若存在实数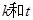 ,满足x
,满足x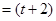 a
a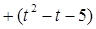 b,y
b,y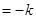 a
a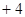 b且x⊥y,求出
b且x⊥y,求出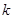 关于
关于 的关系式
的关系式 ;
;
(Ⅱ)根据(Ⅰ)的结论,试求出函数 在
在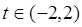 上的最小值.
上的最小值.
(本小题满分8分)设函数 的图象在
的图象在 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求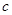 ,
,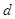 ;
;
(Ⅱ)若函数在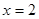 处取得极值
处取得极值 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.
(本小题满分8分)
已知 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足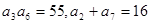 .
.
(Ⅰ)求数列 的通项公式:
的通项公式:
(Ⅱ)等比数列 满足:
满足: ,若数列
,若数列 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分8分)在 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,试求内角B、C的大小.
,试求内角B、C的大小.