（方案二）如图是一个长方体被削去一部分后的多面体的直观图，它的正视图和侧视图已经画出.（单位：cm）.
（Ⅰ）在正视图下面，按照画三视图的要求画出该多面体的俯视图；
（Ⅱ）（普通高中做）求三棱锥
的体积.
(示范性高中做)求多面体
的体积.
（本小题满分10分）
在△ABC中，a、b、c分别是角A、B、C所对的边，且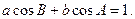
（I）求c；（II）若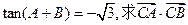
的最大值。
（本小题满分12分）如图，在四棱锥V—ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点。（I）求证：平面EFG//平面VCD；（II）当二面角V—BC—A、V—DC—A分别为45°、30°时，求直线VB与平面EFG所成的角。
如图，已知AD是△ABC的外角ÐEAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连结FB、FC．
（Ⅰ）求证：FB=FC；
（Ⅱ）求证：FB2=FA·FD；
（Ⅲ）若AB是△ABC外接圆的直径，ÐEAC=120°，BC=6cm，求AD的长．
已知函数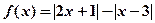
.
（Ⅰ）解不等式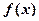
≤4；
（Ⅱ）若存在x使得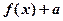
≤0成立，求实数a的取值范围.
在直角坐标系中，以原点O为极点，x 轴为正半轴为极轴，建立极坐标系.
设曲线
（
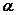为参数）； 直线
.
（Ⅰ）写出曲线
的普通方程和直线l的直角坐标方程；
（Ⅱ）求曲线上的点到直线l的最大距离.