设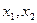 是函数
是函数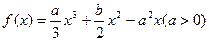 的两个极值点,且
的两个极值点,且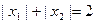 ,
,
(1)证明: ;
;
(2)证明: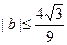 。
。
.(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证: AC 1//平面CDB1;
(II)求二面角C1 -AB-C的平面角的正切值。
-AB-C的平面角的正切值。
(本小题满分12分)已知在△ 中,角
中,角 所对的边分别为
所对的边分别为 ,向
,向
量
(1)若 ,且
,且 平行,求角
平行,求角 的大小;
的大小;
(2)若 ,求
,求 的面积
的面积 .
.
(本小题满分13分)
设 是函数
是函数 的零点,
的零点, .
.
(Ⅰ)求证: ,且
,且
 ;
;
(Ⅱ)求证: .
.
(本小题满分13分)
如图,曲线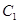 是以原点
是以原点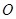 为中心,以
为中心,以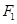 、
、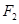 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线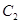 是以
是以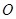 为顶
为顶
点,以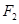 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线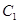 和
和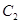 的交点,且
的交点,且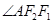 为钝角,若
为钝角,若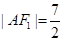 ,
,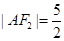 .(Ⅰ)求曲线
.(Ⅰ)求曲线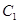 和
和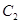 所在的椭圆和抛物线的方程;(Ⅱ)过
所在的椭圆和抛物线的方程;(Ⅱ)过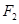 作一条与
作一条与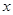 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线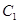 、
、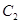 依次交于
依次交于 、
、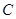 、
、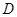 、
、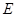 四点(如图),若
四点(如图),若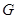 为
为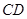 的中点,
的中点,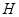 为
为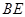 的中点,问
的中点,问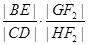 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.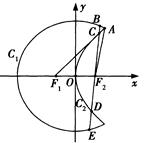
(本小题满分13分)某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若
企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分
别为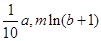 万元(m >0且为常数).已知该企业投放总价值为10万元的A、B
万元(m >0且为常数).已知该企业投放总价值为10万元的A、B
两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(Ⅰ)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(Ⅱ)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?