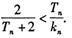（本小题满分12分）
书桌上一共有六本不同的书.问：
（Ⅰ）6本书排成一排，要求其中的2本数学书排在一起，共有多少种不同的排法？
（Ⅱ）6本书分给甲、乙、丙三个同学，每人2本，共有多少种不同方法？
（Ⅲ）(示范性高中做)6本书分给甲、乙、丙三个同学，如果一个人得1本，一个人得2本，一个人得3本，共有多少种不同的分法？
如图，四棱锥P—ABCD的底面为矩形，PA=AD=1，PA⊥面ABCD，E是AB的中点，F为PC上一点，且EF//面PAD。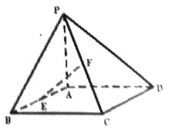
（I）证明：F为PC的中点；
（II）若二面角C—PD—E的平面角的余弦值为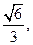
求直线ED与平面PCD所成的角
已知函数
（I）求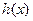
的单调区间；
（II）若函数
的图象上存在一点
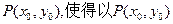为切点的切线的斜率
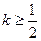成立，求实数a的最大值
如图，某学校要用鲜花布置花圃中ABCDE五个不同区域，要求同一区域上用一种颜色的鲜花，相邻区域使用不同颜色的鲜花，现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择。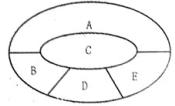
（I）求恰有两个区域用红色鲜花的概率；
（II）记ξ为花圃中用红色鲜花布置区域个数，求随机变量ξ的分布列及其数学期望Eξ.
如图，在△ABC中；角A、B、C所对的边分别是a、b、c，且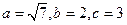
，O为△ABC的外心。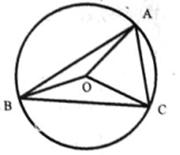
（I）求△ABC的面积；
（II）求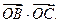
已知数列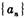
满足：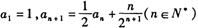
①求数列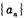
的通项公式；
②证明；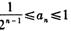
③设
，且
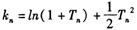，证明