（本小题满分14分）
为积极响应国家“家电下乡”政策的号召，某厂家把总价值为10万元的A、B两种型号的电视机投放市场，并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元，农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴，补贴方案如下表所示，设投放市场的A、B型号电视机的价值分别为
万元,
万元，农民得到的补贴为
万元,解答以下问题.
| |
A型号 |
B型号 |
| 电视机价值(万元) |
|
|
| 农民获得补贴(万元) |
 |
 |
(1) 用的代数式表示
(2) 当取何值时, 取最大值并求出其最大值（精确到0.1，参考数据：
）
锐角三角形ABC的内角A,B,C的对边分别为
(1)求B的大小；
（2）求
的取值范围.
在△ABC中，已知
，
，B=45°， 求A、C及c
如图，已知椭圆
到它的两焦点F1、F2的距离之和为4，A、B分别是它的左顶点和上顶点..
（1）求此椭圆的方程及离心率；
（2）平行于AB的直线l与椭圆相交于P、Q两点，求|PQ|的最大值及此时直线l的方程.
已知，椭圆C以过点A（1，
），两个焦点为（－1，0）（1，0）。
（1）求椭圆C的方程；
（2）E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。
某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是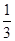
，遇到红灯时停留的时间都是2min.
（1）求这名学生在上学路上到第三个路口时首次遇到红灯的概率；
（2）这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.