(本小题满分14分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线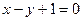 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
某教研机构准备举行一次高中数学新课程研讨会,拟邀请50名使用不同版本的一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
10 |
5 |
(1)假设使用北师大版的5名教师中有3名男教师,2名女教师,若随机选出2名用北师大版的教师发言,求恰好是一男一女的概率P
(3)从这50名教师中随机选出2名教师发言,求第一位发言的教师所使用版本是北师大版的概率P
一个多面体的直观图和三视图如图所示,其中M、G分别是AB、DF的中点。
(1)在AD上(含A、D端点)确定一点P,使得GP//平面FMC;
(2)一只苍蝇在几何体ADF-BCE内自由飞翔,求它飞入几何体F-AMCD内的概率。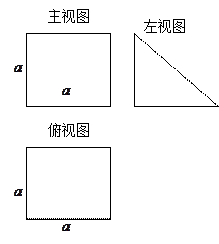

已知函数f(x)=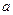 sinx+bcosx的图象经过点(
sinx+bcosx的图象经过点(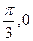 ),(
),(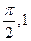 )
)
(1)求实数a和b的值;(2)当x为何值时,f(x)取得最大值。
下面四个命题
(1) 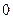 比
比 大
大
(2)两个复数互为共轭复数,当且仅当其和为实数
(3) 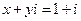 的充要条件为
的充要条件为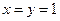
(4)如果让实数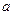 与
与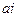 对应,那么实数集与纯虚数集一一对应,
对应,那么实数集与纯虚数集一一对应,
其中正确的命题个数是()
A.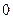 |
B.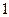 |
C.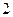 |
D.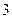 |
已知复数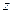 满足:
满足: 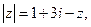 求
求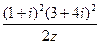 的值.
的值.