(13分)某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且获胜的概率均为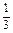 .
.
(1)求这支篮球队首次获胜前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好获胜3场的概率;
(3)求这支篮球队在6场比赛中获胜场数的期望.
(本小题满分14分)设数列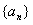 的首项
的首项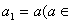 R),且
R),且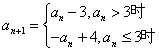 ,
,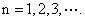 (Ⅰ)若
(Ⅰ)若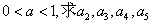 ;(Ⅱ)若
;(Ⅱ)若 ,证明:
,证明: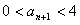 ;(Ⅲ)若
;(Ⅲ)若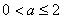 ,求所有的正整数
,求所有的正整数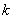 ,使得对于任意
,使得对于任意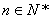 ,均有
,均有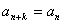 成立.
成立.
(本小题满分14分)
已知函数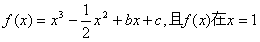 处取得极值.
处取得极值.
(Ⅰ)求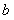 的值;
的值;
(Ⅱ)若当 恒成立,求
恒成立,求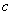 的取值范围;
的取值范围;
(Ⅲ)对任意的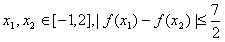 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
(本小题满分13分)已知各项都不相等的等差数列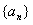 的前六项和为60,且
的前六项和为60,且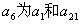 的等比中项.(Ⅰ)求数列
的等比中项.(Ⅰ)求数列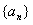 的通项公式
的通项公式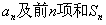 ;(Ⅱ)若数列
;(Ⅱ)若数列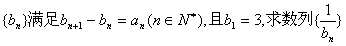 的前
的前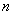 项和
项和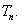
(本小题满分13分)如图,正三棱柱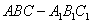 中,D是BC的中点,
中,D是BC的中点,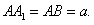
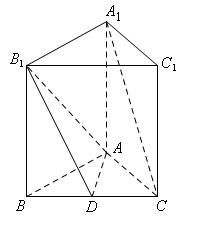
(Ⅰ)求证: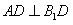 ;(Ⅱ)求证:
;(Ⅱ)求证: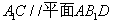 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥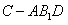 的体积.
的体积.
(本小题13分) 已知函数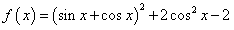 .(Ⅰ)求
.(Ⅰ)求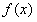 函数图象的对称轴方程;(Ⅱ)求
函数图象的对称轴方程;(Ⅱ)求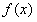 的单调增区间;(Ⅲ)当
的单调增区间;(Ⅲ)当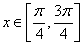 时,求函数
时,求函数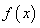 的最大值,最小值.
的最大值,最小值.