由三个电子元件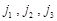 组成的线路系统如右图所示,
组成的线路系统如右图所示,
每个电子元件能正常工作的概率都是t  .
.
(1)求该线路系统正常工作的概率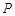 ;
;
(2)试问函数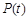 在区间
在区间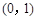 上是否存在最值?
上是否存在最值?
已知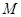 是满足下列性质的所有函数
是满足下列性质的所有函数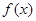 组成的集合:对于函数
组成的集合:对于函数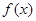 ,使得对函数
,使得对函数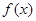 定义域内的任意两个自变量
定义域内的任意两个自变量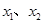 ,均有
,均有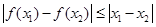 成立.
成立.
(1)已知函数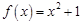 ,
,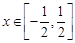 ,判断
,判断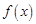 与集合
与集合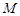 的关系,并说明理由;
的关系,并说明理由;
(2)已知函数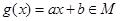 ,求实数
,求实数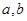 的取值范围;
的取值范围;
(3)是否存在实数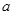 ,使得
,使得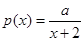 ,
,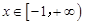 属于集合
属于集合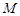 ?若存在,求
?若存在,求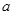 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
我校为进行“阳光运动一小时”活动,计划在一块直角三角形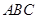 的空地上修建一个占地面积为
的空地上修建一个占地面积为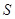 (平方米)的矩形
(平方米)的矩形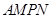 健身场地.如图,点
健身场地.如图,点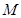 在
在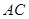 上,点
上,点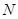 在
在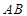 上,且
上,且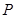 点在斜边
点在斜边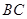 上.已知
上.已知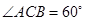 ,
,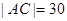 米,
米,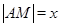 米,
米, .设矩形
.设矩形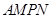 健身场地每平方米的造价为
健身场地每平方米的造价为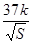 元,再把矩形
元,再把矩形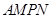 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为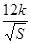 元(
元(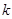 为正常数).
为正常数).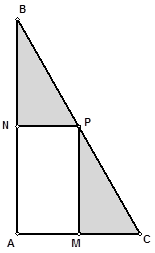
(1)试用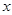 表示
表示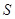 ,并求
,并求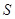 的取值范围;
的取值范围;
(2)求总造价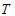 关于面积
关于面积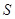 的函数
的函数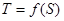 ;
;
(3)如何选取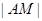 ,使总造价
,使总造价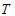 最低(不要求求出最低造价).
最低(不要求求出最低造价).
设集合 ,
, 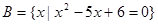 ,
, 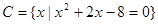 .
.
(1)若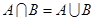 ,求实数
,求实数 的值;
的值;
(2)若 ,且
,且 ,求实数
,求实数 的值;
的值;
(3)若 ,求实数
,求实数 的值.
的值.
已知集合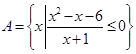 ,集合
,集合 .
.
(1)求集合 与集合
与集合 ;
;
(2)若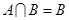 ,求实数
,求实数 的取值范围.
的取值范围.
解关于 的不等式:
的不等式: .
.