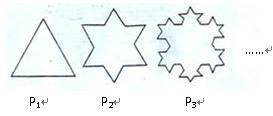
(本小题10分)“雪花曲线”因其形状类似雪花而得名,它可以以下列方式产生,如图,有一列曲线 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(
的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉( ).
).
(1)记曲线 的边长和边数分别为
的边长和边数分别为 和
和 (
(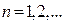 ),求
),求 和
和 的表达式;
的表达式;
(2)记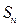 为曲线
为曲线 所围成图形的面积,写出
所围成图形的面积,写出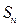 与
与 的递推关系式,并求
的递推关系式,并求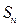 .
.
在△ABC中,角A,B,C所对的边分别为a,b,c,角A,B,C依次成等差数列.
(1)若b2=ac,试判断△ABC的形状;
(2)若△ABC为钝角三角形,且a>c,求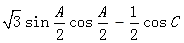 的取值范围.
的取值范围.
设函数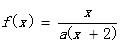 方程f(x)=x有唯一的解,
方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且
(1)求证:数列{ }是等差数列;
}是等差数列;
(2)若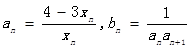 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn;
(3)在(2)的冬件下,若不等式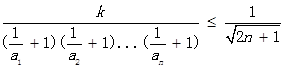 对一切n∈N﹡
对一切n∈N﹡
均成立,求k的最大值.
已知椭圆C的中点在原点,焦点在x轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(1)求椭圆C的方程;
(2)点P(2,3),Q(2,-3)在椭圆上,A、B是椭圆上位
于直线PQ两侧的动点,
(i)若直线AB的斜率为 ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
(ii)当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.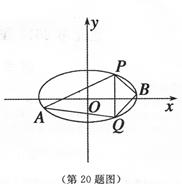
如图所示,三棱柱ABC—A1B1Cl中,AB=AC=AA1=2,面ABC1⊥面AAlClC,∠AAlCl=∠BAC1=600,AC1与A1C相交于0.
(1)求证.BO上面AAlClC;
(2)求三棱锥C1—ABC的体积;
(3)求二面角A1—B1C1—A的余弦值.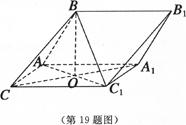
设函数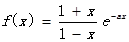
(1)写出定义域及f′(x)的解析式,
(2)设a>O,讨论函数y=f(x)的单调性.