已知数列 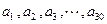 ,其中
,其中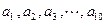 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为  的等差数列;
的等差数列;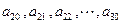 是公差为
是公差为  的等差数列(
的等差数列( ).
).
(1)若 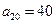 ,求
,求  ;
;
(2)试写出 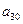 关于
关于  的关系式;
的关系式;
(3)续写已知数列,使得 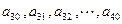 是公差为
是公差为 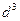 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题,并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题,并进行研究,你能得到什么样的结论?
在复平面上,设点A、B、C 对应的复数分别为  。过A、B、C 三个点做平行四边形。 求第四个顶点D的坐标及此平行四边形的对角线的长。
。过A、B、C 三个点做平行四边形。 求第四个顶点D的坐标及此平行四边形的对角线的长。
已知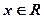 ,
, ,
, 。求证
。求证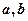 中至少有一个不小于0。
中至少有一个不小于0。
(本小题满分15分)
如图,已知抛物线 的准线为
的准线为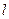 ,
, 为
为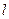 上的一个动点,过点
上的一个动点,过点 作抛物
作抛物
线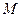 的两条切线,切点分别为
的两条切线,切点分别为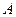 ,
, ,再分别过
,再分别过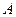 ,
, 两点作
两点作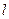 的垂线,垂足分别为
的垂线,垂足分别为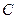 ,
, .
.
(1)求证:直线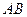 必经过
必经过 轴上的一个定点
轴上的一个定点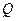 ,并写出点
,并写出点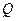 的坐标;
的坐标;
(2)若 ,
,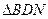 ,
, 的面积依次构成等差数列,求此时点
的面积依次构成等差数列,求此时点 的坐标.
的坐标.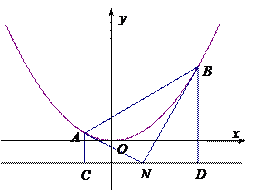
已知函数 是不同时为零的常数),其导函数为
是不同时为零的常数),其导函数为 。
。
(1)当a= 时,若存在
时,若存在 ,使得
,使得 >0成立,求b的取值范围;
>0成立,求b的取值范围;
(2)求证:函数y= 在(-1,0)内至少存在一个零点;
在(-1,0)内至少存在一个零点;
(3)若函数f(x)为奇函数,且在x=1处的切线垂直于直线x+2y-3="0," 关于x的方程 在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围。
在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围。