一个盒子中装有5个编号依次为1、2、3、4、5的球,这5个球除号码外完全相同,有放回的连续抽取两次,每次任意地取出一个球。
(1)求事件A=“取出球的号码之和不小于6”的概率。
(2)设第一次取出的球号码为x,第二次取出的球号码为y,求事件B=“点(x,y)落在直线y =" x+1" 上方”的概率。
已知 在同一平面内,且
在同一平面内,且 .
.
(1)若 ,且
,且 ,求
,求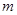 的值;
的值;
(2)若 ,且
,且 ,求向量
,求向量 与
与 的夹角.
的夹角.
一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各一个,这些球除颜色外都相同.
(1)求搅匀后从中任意摸出1个球,恰好是红球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,求至少有一次摸出的球是红球的概率.
在等差数列 中,
中,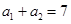 ,
,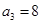 .令
.令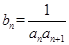 ,数列
,数列 的前
的前 项和为
项和为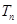 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和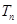 ;
;
(3)是否存在正整数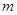 ,
, (
(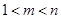 ),使得
),使得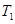 ,
, ,
,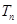 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的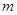 ,
, 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
在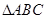 中,角
中,角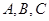 的对边分别为
的对边分别为 ,且
,且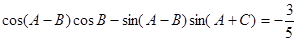
(Ⅰ)求 的值;
的值;
(Ⅱ)若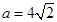 ,
,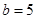 ,求向量
,求向量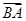 在
在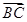 方向上的投影.
方向上的投影.
设向量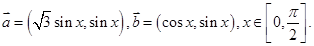
(I)若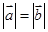 ,求
,求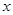 的值;
的值;
(II)设函数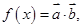 求
求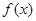 的最大值及
的最大值及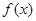 的单调递增区间.
的单调递增区间.