(本题16分)如图,某大风车的半径为2米,每12秒沿逆时针方向旋转一周,它的最底点 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点 开始,运动t秒后与地面距离为h米,
开始,运动t秒后与地面距离为h米,
(1)求函数h=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点);
(2) A从最底点 开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?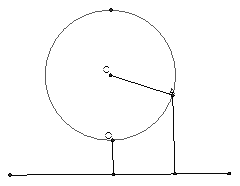
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
已知 是定义在
是定义在 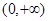 上的增函数,且对任意的
上的增函数,且对任意的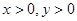 都满足
都满足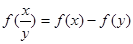 .
.
(Ⅰ)求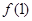 的值;(Ⅱ)若
的值;(Ⅱ)若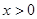 ,证明
,证明 ;
;
(Ⅲ)若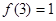 ,解不等式
,解不等式 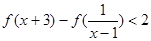 .
.
设命题 函数
函数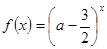 是
是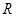 上的减函数,命题
上的减函数,命题 函数
函数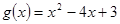 ,
, 的值域为
的值域为 ,若“
,若“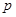 且
且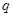 ”为假命题,“
”为假命题,“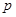 或
或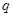 ”为真命题,求实数
”为真命题,求实数 的取值范围.
的取值范围.
设椭圆C:
 过点
过点 , 且离心率
, 且离心率 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过右焦点 的动直线交椭圆于点
的动直线交椭圆于点 ,设椭圆的左顶点为
,设椭圆的左顶点为 连接
连接 且交直线
且交直线 于
于 ,若以MN为直径的圆恒过右焦点F,求
,若以MN为直径的圆恒过右焦点F,求 的值
的值
某校高一某班的一次数学测试成绩(满分100分)的茎叶图和频率分布直方图都受到不同程度的污染,但可见部分如下,据此解答如下问题:
(Ⅰ) 求分数在[50,60)的频率及全班人数;
(Ⅱ) 求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.