已知圆C：
，问是否存在斜率为1的直线
，使被圆C截得的弦为AB，以AB为直径的圆经过原点，若存在，写出直线的方程；若不存在，说明理由
已知直线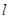
的极坐标方程为
，圆C的参数方程为
，求直线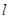被圆截得的弦长。
已知函数
在点
处取得极值。
（1）求实数a的值；
（2）若关于x的方程
在区间[0，2]上有两个不等实根，求b的取值范围；
（3）证明：对于任意的正整数
，不等式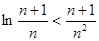
。
已知椭圆C的中心在坐标原点，焦点在x轴上，离心率为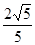
，它的一个顶点恰好是抛物线
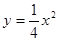的焦点。
（1）求椭圆C的标准方程；
（2）过椭圆C的右焦点作直线l交椭圆C于A、B两点，交y轴于M点，若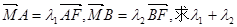
的值。
某研究小组在电脑上进行人工降雨摸拟试验，准备用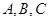
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨，其试验数据统计如下：
| 方式 |
实施地点 |
大雨 |
中雨 |
小雨 |
摸拟试验总次数 |
 |
甲 |
4次 |
6次 |
2次 |
12次 |
 |
乙 |
3次 |
6次 |
3次 |
12次 |
 |
丙 |
2次 |
2次 |
8次 |
12次 |
假设甲、乙、丙三地实施的人工降雨彼此互不影响．
（Ⅰ）求甲、乙两地恰为中雨且丙地为小雨的概率；
（Ⅱ）考虑到旱情和水土流失，如果甲地恰需中雨即能达到理想状态，乙地必须是大雨才能达到理想状态，丙地只要是小雨或中雨就能达到理想状态，求甲、乙、丙三地中至少有两地降雨量达到理想状态的概率．
，且x是第二象限的角，