已知( 的展开式中,第4项的二项式系数与第5项的二项式系数之比为1:3,求二项式系数最大的项。
的展开式中,第4项的二项式系数与第5项的二项式系数之比为1:3,求二项式系数最大的项。
已知函数 ,
,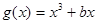
(1)若曲线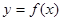 与曲线
与曲线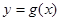 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求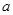 ,
,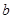 的值;
的值;
(2)当 ,
,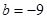 时,若函数
时,若函数 在区间[
在区间[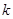 ,2]上的最大值为28,求
,2]上的最大值为28,求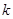 的取值范围.
的取值范围.
设 的导数为
的导数为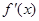 ,若函数
,若函数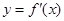 的图像关于直
的图像关于直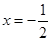 对称,且
对称,且 . (1)求实数
. (1)求实数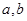 的值 ;(2)求函数
的值 ;(2)求函数 的极值.
的极值.
(1)用1、2、3、4、5、6、7可组成多少个无重复数字的四位数且四位数为偶数;
(2)用0、1、2、3、4、5可组成多少无重复数字的且可被5整除的五位数. (用数字作答)
已知数列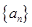 的前n项和
的前n项和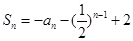 (n为正整数).
(n为正整数).
(1)令 ,求证数列
,求证数列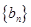 是等差数列;
是等差数列;
(2)求数列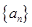 的通项公式;
的通项公式;
(3)令 ,
, 。是否存在最小的正整数
。是否存在最小的正整数 ,使得对于
,使得对于 都有
都有 恒成立,若存在,求出
恒成立,若存在,求出 的值。不存在,请说明理由.
的值。不存在,请说明理由.
设数列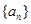 的前
的前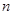 项和为
项和为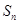 ,
,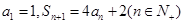 .
.
(1)若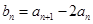 ,求
,求 ;
;
(2)若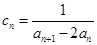 ,求
,求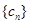 的前6项和
的前6项和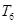 .
.