已知函数 ,
,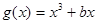
(1)若曲线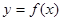 与曲线
与曲线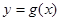 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求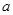 ,
,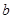 的值;
的值;
(2)当 ,
,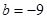 时,若函数
时,若函数 在区间[
在区间[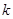 ,2]上的最大值为28,求
,2]上的最大值为28,求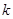 的取值范围.
的取值范围.
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为 和
和 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
① |
0.16 |
| 70.5~80.5 |
10 |
?② |
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
③ |
④ |
| 合计 |
50 |
1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为
000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格①②③④并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
某射手在一次射击中射中10环、9环、8环、7环, 7环以下的概率
分别为0.24,0.28,0.19,0.16,0.13,计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不是8环的概率。
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上。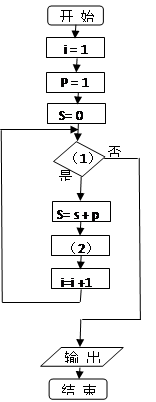
程序语言:
i=1
p=1
s=0
DO
s=" s" + p
(2)
i=i+1
(3)
PRINT s
END
(1)_________ (2)______(3)
已知三棱锥S—ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.
(1)求证:BC⊥SA
(2)若S在底面ABC内的射影为O,证明:O为底面△ABC的中心;
(3)若二面角H—AB—C的平面角等于30°,SA=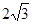 ,求三棱锥S—ABC的体积.
,求三棱锥S—ABC的体积.