(本小题满分14分)已知区域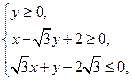 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率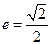 .
.
⑴求圆C及椭圆C1的方程;
⑵设圆 与
与 轴正半轴交于点D,
轴正半轴交于点D, 点为坐标原点,
点为坐标原点,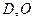 中点为
中点为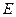 ,问是否存在直线
,问是否存在直线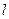 与椭圆
与椭圆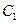 交于
交于 两点,且
两点,且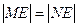 ?若存在,求出直线
?若存在,求出直线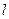 与
与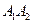 夹角
夹角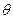 的正切值的取值范围;若不存在,请说明理由.
的正切值的取值范围;若不存在,请说明理由.
(本小题满分12分)某驾校为了保证学员科目二考试的通过率,要求学员在参加正式考试(下面简称正考)之 前必须参加预备考试(简称预考),且在预考过程中评分标准得以细化,预考成绩合格者才能参加正考.现将10名学员的预考成绩绘制成茎叶图,规定预考成绩85分以上为合格,不低于90分为优秀。若上述数据的中位数为85.5,平均数为83.
(Ⅰ)求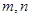 的值,指出该组数据的众数,并根据平均数以及参加正考的成绩标准对该驾校学员的学习情况作简单评价;
的值,指出该组数据的众数,并根据平均数以及参加正考的成绩标准对该驾校学员的学习情况作简单评价;
(Ⅱ)若在上述可以参加正考的学员中随机抽取2人,求其中恰有一人成绩优秀的概率.
(本小题满分12分)设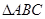 的内角
的内角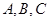 所对的边为
所对的边为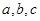 ,
,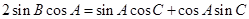
(1)求角 的大小;
的大小;
(2)若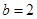 ,
,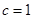 ,
,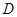 为
为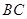 的中点,求
的中点,求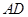 的长.
的长.
选修4—5:不等式选讲(本小题满分10分)
已知函数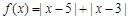 .
.
(1)求函数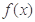 的最小值
的最小值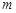 ;
;
(2)若正实数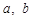 满足
满足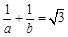 ,求证:
,求证: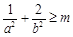 .
.
选修4 - 4:坐标系与参数方程(本小题满分10分)
在极坐标系中,曲线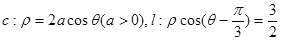 ,
, 有且仅有一个公共点.
有且仅有一个公共点.
(1)求 ;
;
(2) 为极点,
为极点, 为曲线
为曲线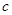 上的两点,且
上的两点,且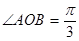 ,求
,求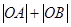 的最大值.
的最大值.
(本小题满分12分)已知函数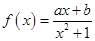 在点
在点 处的切线方程为
处的切线方程为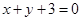 .
.
(1)求函数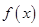 的解析式;
的解析式;
(2)设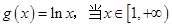 时,求证:
时,求证: ;
;
(3)已知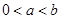 ,求证:
,求证: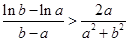 .
.