(本小题满分14分)设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}是等差数列,数列{bn―2}是等比数列(n∈N*).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)是否存在k∈N*,使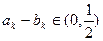 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.
(本小题满分10分)
已知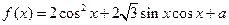 ,
,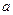 为实常数。
为实常数。
(I)求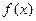 的最小正周期;
的最小正周期;
(II)若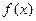 在
在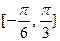 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求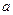 的值。
的值。
(本小题满分10分)
已知数列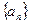 中,
中,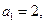 且点P
且点P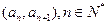 在直线
在直线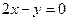 上.
上.
(1)求数列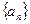 的通项公式;
的通项公式;
(2)设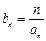 ,求数列
,求数列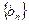 的前
的前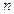 项和
项和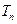 .
.
(本小题满分10分)
设函数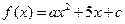
(1)若不等式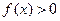 的解集是
的解集是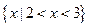 ,求不等式
,求不等式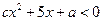 的解集;
的解集;
(2)当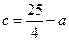 时,
时, 恒成立,求实数
恒成立,求实数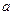 的取值范围.
的取值范围.
(本小题满分10分)
设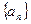 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和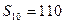
且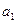 ,
,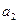 ,
,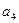 成等比数列,求公差
成等比数列,求公差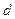 的值和数列
的值和数列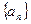 的通项公式.
的通项公式.
(本小题满分8分)
临汾市染料厂生产化工原料,当年产量在150吨到250吨时,年生产总成本y(万元)与年产量x(吨)之间的关系可近似表示为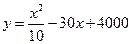 ,为使每吨平均成本最低,年产量指标应定在多少吨?(注:平均成本
,为使每吨平均成本最低,年产量指标应定在多少吨?(注:平均成本 )
)