(本小题满分12分)现有分别写有数字1,2,3,4,5的5张白色卡片、5张黄色卡片、5张红色卡片。每次试验抽一张卡片,并定义随机变量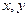 如下:若是白色,则
如下:若是白色,则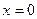 ;若是黄色,则
;若是黄色,则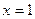 ;若是红色,则
;若是红色,则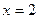 ;若卡片数字是
;若卡片数字是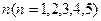 ,则
,则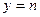
(1)求概率
(2)求数字期望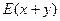 与数字方差
与数字方差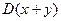
如图,点 为斜三棱柱
为斜三棱柱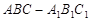 的侧棱
的侧棱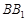 上一点,
上一点,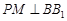 交
交 于点
于点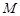 ,
,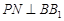 交
交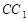 于点
于点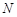 .
.
(1) 求证: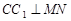 ;
;
(2) 在任意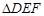 中有余弦定理:
中有余弦定理: .
.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明
已知二次函数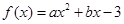 在
在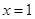 处取得极值,且在
处取得极值,且在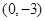 点处的切线与直线
点处的切线与直线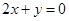 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数 在
在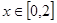 的最值。
的最值。
有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.
已知复数z=(2+i)m2--2(1-i).当实数m取什么值时,复数z是:
(1)虚数;(2)纯虚数;(3)复平面内第二、四象限角平分线上的点对应的复数?
已知函数 .
.
(1)试判断函数 的单调性;
的单调性;
(2)设 ,求
,求 在
在 上的最大值;
上的最大值;
(3)试证明:对 ,不等式
,不等式 .
.