已知函数 ,且
,且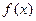 在
在 处取得极值.
处取得极值.
(1)求 的值;
的值;
(2)若当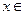 [-1,
[-1, ]时,
]时,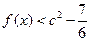 恒成立,求
恒成立,求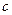 的取值范围.
的取值范围.
设函数
.
(Ⅰ)若当
时
取得极值,求
的值,并讨论
的单调性;
(Ⅱ)若
存在极值,求
的取值范围,并证明所有极值之和大于
.
如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
. 假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10 000个点,以X表示落入M中的点的数目.
(Ⅰ)求X的均值EX;
(Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间(-0.03,0.03)内的概率.
附表:


在平面直角坐标系
中,经过点
且斜率为
的直线
与椭圆
有两个不同的交点
和
.
(Ⅰ)求
的取值范围;
(Ⅱ)设椭圆与
轴正半轴、
轴正半轴的交点分别为
、
,是否存在常数
,使得向量
与
共线?如果存在,求
值;如果不存在,请说明理由.
如图,在三棱锥
中, 侧面
与侧面
均为等边三角形,
,
为
中点.
(Ⅰ)证明:
平面
(Ⅱ)求二面角
的余弦值. 
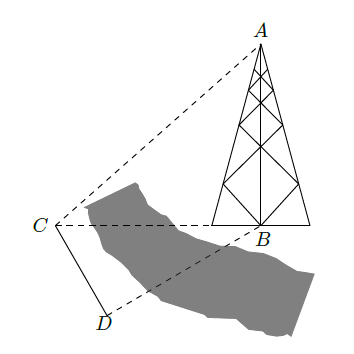
如图,测量河对岸的塔高
时,可以选与塔底
在同一水平面内的两个测点
与
. 现测得
,
,
,并在点
测得塔顶
的仰角为
,求塔高
.