甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为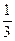 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为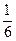 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为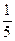 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;


(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
(本小题满分10分)
若关于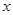 的不等式
的不等式 的解集为非空集合,求实数
的解集为非空集合,求实数 的取值范围。
的取值范围。
(本小题满分10分)
在直角坐标系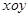 中,直线
中,直线 :
: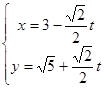 (
(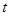 为参数),在极坐标系中(以原点为极点,以
为参数),在极坐标系中(以原点为极点,以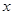 轴正半轴为极轴),圆C的方程:
轴正半轴为极轴),圆C的方程: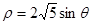
(1)求圆C的直角坐标方程;
(2)设圆C与直线 交于
交于 ,
,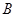 两点,点
两点,点 的坐标
的坐标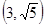 ,求
,求
(本小题满分10分)
已知:如图, 中,
中, ,
,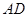 ,
, 是角平分线。求证:
是角平分线。求证: 。
。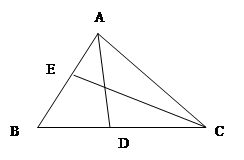
(本小题满分12分)已知函数 ,
,
(1)若 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(2)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 ,
, ,问是否存在点
,问是否存在点 ,使
,使 在
在 处的切线与
处的切线与 在
在 处的切线平行?若存在,求
处的切线平行?若存在,求 的横坐标,若不存在,请说明理由。
的横坐标,若不存在,请说明理由。
(本小题满分12分)设圆C: ,此圆与抛物线
,此圆与抛物线
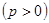 有四个不同的交点,若在
有四个不同的交点,若在 轴上方的两交点分别为
轴上方的两交点分别为 ,
,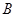 ,坐标原点为
,坐标原点为 ,
,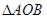 的面积为
的面积为 。
。
(1)求实数 的取值范围;
的取值范围;
(2)求 关于
关于 的函数
的函数 的表达式及
的表达式及 的取值范围。
的取值范围。