(本小题满分16分)已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有
(1)求a3,a5;
(2)设 (n∈N*),证明:数列{bn}是等差数列;
(n∈N*),证明:数列{bn}是等差数列;
(3)设cn=
 qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
(本小题满分14分)
已知椭圆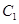 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,
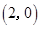 ,点
,点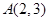 在椭圆
在椭圆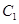 上,过点
上,过点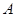 的直线
的直线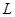 与抛物线
与抛物线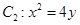 交于
交于 两点,抛物线
两点,抛物线 在点
在点 处的切线分别为
处的切线分别为 ,且
,且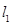 与
与 交于点
交于点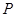 .
.
(1) 求椭圆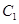 的方程;
的方程;
(2) 是否存在满足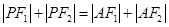 的点
的点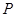 ? 若存在,指出这样的点
? 若存在,指出这样的点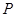 有几个(不必求出点
有几个(不必求出点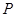 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
(本小题满分14分)
已知数列 的前
的前 项和为
项和为 ,且
,且  N
N .
.
(1) 求数列 的通项公式;
的通项公式;
(2)若 是三个互不相等的正整数,且
是三个互不相等的正整数,且 成等差数列,试判断
成等差数列,试判断 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.
(本小题满分14分)
如图4,在三棱柱 中,△
中,△ 是边长为
是边长为 的等边三角形,
的等边三角形, 平面
平面 ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点. 
(1)求证: ∥平面
∥平面 ;
;
(2)若 为
为 上的动点,当
上的动点,当 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 时,
时,
求平面 与平面
与平面 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 |
0 |
1 |
2 |
3 |
 |
 |
 |
 |
 |
(1) 求至少有一位学生做对该题的概率;
(2) 求 ,
, 的值;
的值;
(3) 求 的数学期望.
的数学期望.
(本小题满分12分)
已知函数 (其中
(其中 ,
, ,
, )的最大值为2,最小正周
)的最大值为2,最小正周
期为 .
.
(1)求函数 的解析式;
的解析式;
(2)若函数 图象上的两点
图象上的两点 的横坐标依次为
的横坐标依次为 ,
, 为坐标原点,求△
为坐标原点,求△ 的
的
面积.