(本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;若将频率视为概率,对甲学生在培训后参加的一次数学竞赛成绩进行预测,求甲的成绩高于80分的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
标准差公式: .
.
在 中,角
中,角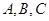 所对的边分别为
所对的边分别为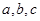 ,且满足
,且满足 ,
,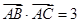 .
.
(1)求 的面积;
的面积;
(2) 若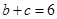 ,求
,求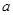 的值.
的值.
在数列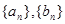 中,
中, ,且
,且 成等差数列,
成等差数列, 成等比数列
成等比数列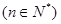 。
。
(1)求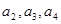 及
及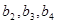 ,由此猜测
,由此猜测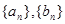 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明: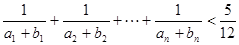 。
。
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,决出胜负即停止比赛。按以往的比赛经验,每局比赛中,甲胜乙的概率为 。
。
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设比赛的局数为X,求X的分布列和数学期望。
将一个质地均匀的正方体(六个面上分别标有数字0,1,2,3,4,5)和一个正四面体(四个面分别标有数字1,2,3,4)同时抛掷一次,规定“正方体向上的面上的数字为a,正四面体的三个侧面上的数字之和为b”。设复数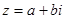 。
。
(1)若集合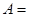 {
{ 为纯虚数},用列举法表示集合A;
为纯虚数},用列举法表示集合A;
(2)求事件“复数在复平面内对应的点(a,b)满足 ”的概率。
”的概率。
已知 ,求(请写出最后结果):
,求(请写出最后结果):
(1) ;
;
(2)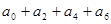 ;
;
(3) 。
。